K-D Tree基础

什么是K-D Tree？

k-D Tree(KDT , k-Dimension Tree) 是一种可以 高效处理 \(k\) 维空间信息 的数据结构，常用于 领域查询，最近点对查询 等操作。

k-D Tree具有二叉搜索树的形态，其每个节点都对应 \(k\) 维空间内的一个点。

在题目中，一般 \(k=2\)。

节点信息储存

我们通常用一个结构体储存k-D Tree所有节点的信息

1
2
3
4
5
6
7
8
9
//假设维护的是K维的空间信息
struct node
{
    int d[K];//d[i]表示第i+1维的坐标（因为下标从0开始）
    int mx[K],mn[K];//mx[i]和mn[i]表示该节点所管辖的第i+1维坐标极值,比较关键，后面会讲
    int ls,rs;//左右儿子
	int val;//节点权值，可能会用到
    int sum;//节点子树的权值和，可能会用到
}t[MAX],ori[MAX];//t为k-D Tree所使用的数组

建树

k-D Tree常见的建树方式有两种：交替建树，方差建树。

交替建树代码实现简单，容易记忆，而方差建树较为复杂，用的较少，故这里只介绍交替建树的方法。

交替建树

交替建树有以下几个步骤：

  1. 将当前点集的所有点按第 \(d\) 维排序，取出中位数。
  2. 将取出的中位数作为当前点集的根节点，剩余的点集分别作为该点的左子树和右子树。
  3. 重复以上两个步骤，每次 \(d\) 要改成 \(d+1\)，如果 \(d+1\gt k\) ，则 \(d=1\)（其中 \(k\) 为所有点的维度），直到所有树上的所有点都确定。

有点抽象？不怕！举个例子就懂了！

给出 \(7\) 个 \(2\) 维空间的点，分别为 \((1,4),(2,5),(1,5),(2,3),(3,1),(4,1),(3,4)\)。

首先按第 \(1\) 维排序，得到的点集是 \((1,4),(1,5),(2,5),(2,3),(3,1),(3,4),(4,1)\)。

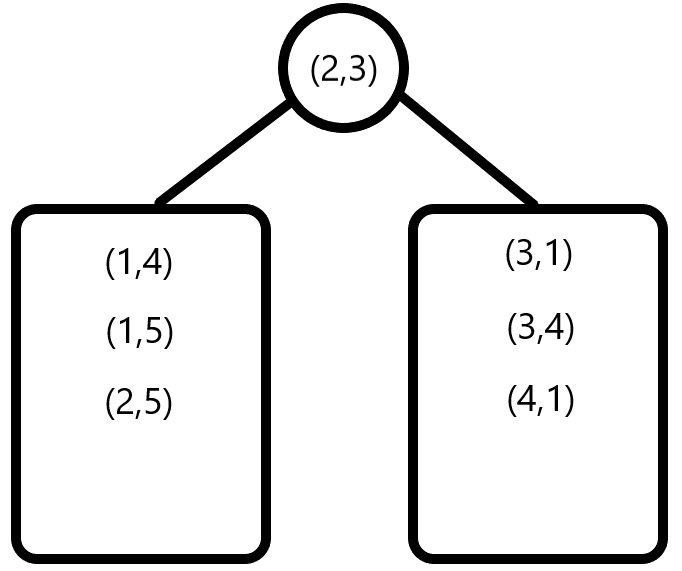
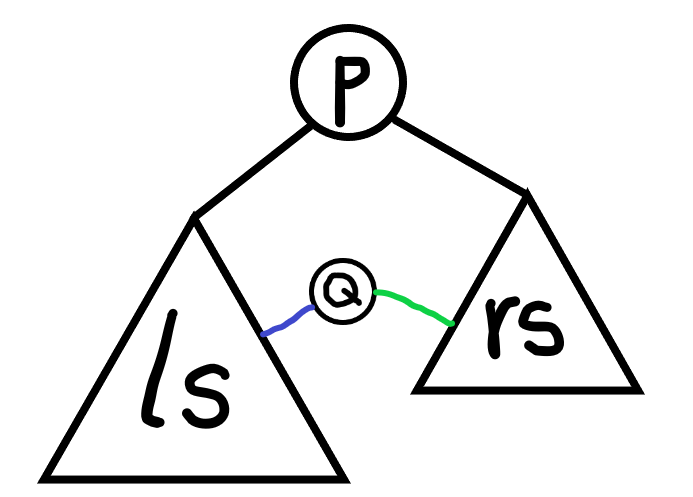
取出中位数 \((2,3)\)，作为当前点集的根节点，剩余的点集分别作为左子树和右子树，如图：

对于剩下的两个点集，我们继续建树，此时我们要对第 \(2\) 维排序。

然后得到两个点集，\((1,4),(1,5),(2,5)\) 和 \((3,1),(4,1),(3,4)\)。

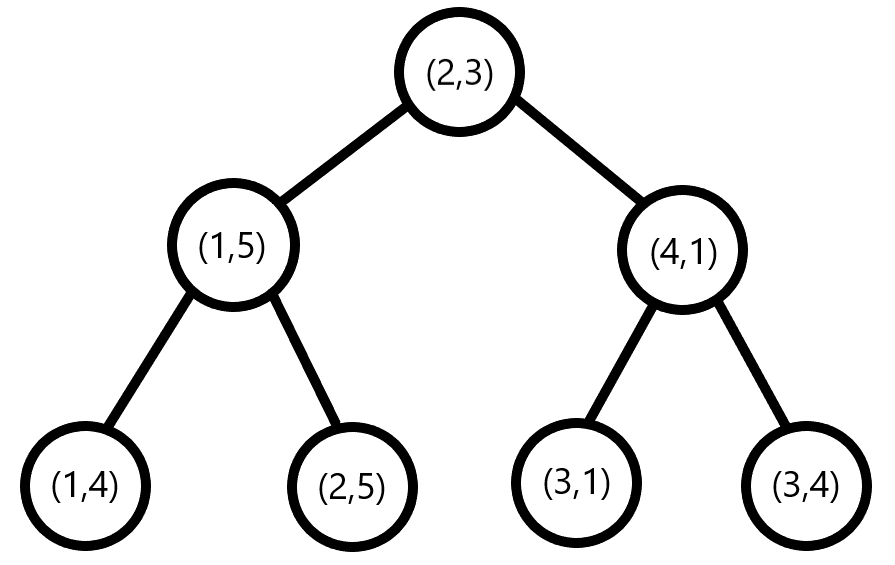
分别取出中位数 \((1,5)\) 和 \((4,1)\) 作为两个点集的根节点，剩余的点集继续建树，最后得到的树如图所示：

这样，我们就通过 交替建树 的方式得到了一颗层数为 \(\log n\) 的 k-D Tree。

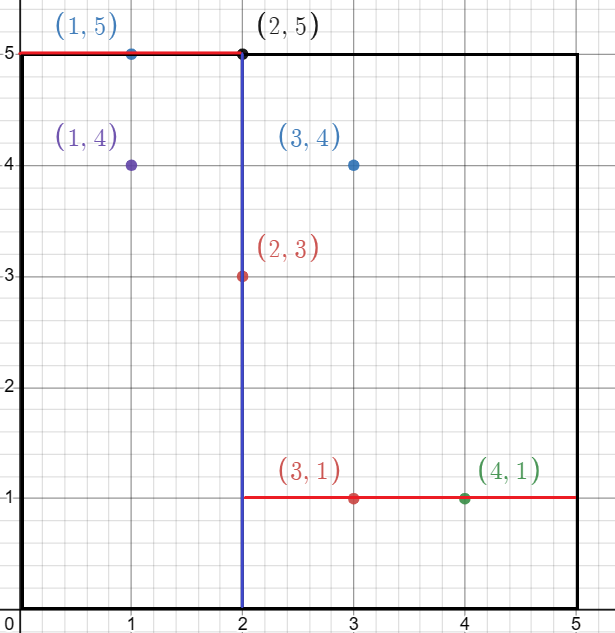
这一过程可以用一个平面直角坐标系来表示：

找中位数是个比较棘手的事情，我们当然可以使用 sort() 排序，然后找到位置为 mid 的元素，但是这样的时间复杂度是 \(O(n\log n)\)。

我们其实还可以使用这样一个函数 nth_element() ，将 l 和 r 之间的数按照比较规则 cmp 排序后，位置为 mid 的元素就是中位数，像这样 nth_element(ori+l,ori+mid,ori+r+1,cmp)。这样的时间复杂度是 \(O(\log n)\)。

k-D Tree建树整体的复杂度是 \(O(n\log n)\)。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int K;//排序时的维度
bool cmp(node a,node b)
{
    return a.d[K]<b.d[K];//按第K维排序
}
int build(int l,int r,int k)//l,r分别是集合的边界,k是排序时的维度
{
    if(l>r)return 0;
    int mid=(l+r)>>1;
    K=k;
    nth_element(ori+l,ori+mid,ori+r+1,cmp);//ori为点集
    t[mid]=ori[mid];//t为k-D Tree所使用的数组
    t[mid].ls=build(l,mid-1,k^1);//k^1,切换维度，交替建树
    t[mid].rs=build(mid+1,r,k^1);
    update(mid);//合并子树信息，后面会讲
    return mid;//返回节点编号
}

子树信息合并

每个节点都需要维护 mx[i] 和 mn[i] ， 即该节点所管辖的第 \(i+1\) 维坐标极值。

对于 \(2\) 维的 k-D Tree，(mx[0],mx[1]),(mn[0],mx[1]),(mx[0],mn[1]),(mn[0],mn[1]) 这四个点可以看作该节点所管辖矩形的四个顶点。

合并起来比较类似于线段树，看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void update(int p)
{
    int ls=t[p].ls;
    int rs=t[p].rs;
    t[p].sum=t[ls].sum+t[rs].sum+t[p].val;//维护节点权值和，可能会用到
    for(int i=0;i<K;i++)//K为所有点的维度，例如平面上的点的K就是2
    {
        t[p].mx[i]=t[p].mn[i]=t[p].d[i];//初始化
        if(ls)
        {
            t[p].mx[i]=max(t[p].mx[i],t[ls].mx[i]);
            t[p].mn[i]=min(t[p].mn[i],t[ls].mn[i]);
        }
        if(rs)
        {
            t[p].mx[i]=max(t[p].mx[i],t[rs].mx[i]);
            t[p].mn[i]=min(t[p].mn[i],t[rs].mn[i]);
        }
        //这里比较容易写错，需要细心检查
    }
}

mx[i] 和 mn[i] 非常关键，合理使用能极大优化查询时的复杂度。

下面放一个只需要建树和简单的查询的小k-D Tree模板题

洛谷 P4475 巧克力王国

给出 \(n\) 个二元组 \((x,y)\) ，每个二元组有一个权值 \(h\)，现有 \(m\) 次询问，每次给出 \(a,b,c\)，询问所有满足 \(ax+by\lt c\) 的二元组的权值和。

题解：

每个二元组可以抽象成平面上的点，使用k-D Tree来维护，建树就不用说了，把权值和维护上就行，现在主要来说查询。

我们已经维护了 mx[i] 和 mn[i] ，如果当前节点管辖的矩形的四个顶点都满足 \(ax+by\lt c\)，说明该节点子树中的所有节点都满足 \(ax+by\lt c\)，直接返回权值和即可；如果都不满足，说明子树中的所有节点都不满足，直接返回 \(0\)。否则就像线段树一样，递归左右子树统计答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int query(int x)
{
	int tot=0;
	tot+=check(t[x].mx[0],t[x].mx[1]);
	tot+=check(t[x].mn[0],t[x].mn[1]);
	tot+=check(t[x].mx[0],t[x].mn[1]);
	tot+=check(t[x].mn[0],t[x].mx[1]);
	if(tot==4)return t[x].sum;//当前节点管辖的矩形满足 ax+by<c
	if(tot==0)return 0;//都不满足
	int ans=0;//ans为答案
	if(check(t[x].d[0],t[x].d[1]))ans+=t[x].val;//该节点满足 ax+by<c，先加上这个节点的权值
	if(t[x].ls)ans+=query(t[x].ls);//递归左子树
	if(t[x].rs)ans+=query(t[x].rs);//递归右子树
	return ans;
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAX=5e4+4;
int a,b,c,K;
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
struct node
{
	int d[5];
	int mx[5],mn[5];
	int val,sum,ls,rs;
}ori[MAX],t[MAX];
bool cmp(node a,node b)
{
	return a.d[K]<b.d[K];
}
bool check(int x,int y)
{
	return a*x+b*y<c;
}
void update(int x)
{
	int ls=t[x].ls;
	int rs=t[x].rs;
	for(int i=0;i<=1;i++)
	{
		t[x].mx[i]=t[x].mn[i]=t[x].d[i];
		if(ls)
		{
			t[x].mx[i]=max(t[x].mx[i],t[ls].mx[i]);
			t[x].mn[i]=min(t[x].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[x].mx[i]=max(t[x].mx[i],t[rs].mx[i]);
			t[x].mn[i]=min(t[x].mn[i],t[rs].mn[i]);
		}
	}
	t[x].sum=t[ls].sum+t[rs].sum+t[x].val;
}
int build(int l,int r,int k)
{
	if(l>r)return 0;
	int mid=(l+r)>>1;
	K=k;
	nth_element(ori+l,ori+mid,ori+r+1,cmp);
	t[mid]=ori[mid];
	if(l<mid)t[mid].ls=build(l,mid-1,k^1);
	if(r>mid)t[mid].rs=build(mid+1,r,k^1);
	update(mid);
	return mid;
}
int query(int x)
{
	int tot=0;
	tot+=check(t[x].mx[0],t[x].mx[1]);
	tot+=check(t[x].mn[0],t[x].mn[1]);
	tot+=check(t[x].mx[0],t[x].mn[1]);
	tot+=check(t[x].mn[0],t[x].mx[1]);
	if(tot==4)return t[x].sum;
	if(tot==0)return 0;
	int ans=0;
	if(check(t[x].d[0],t[x].d[1]))ans+=t[x].val;
	if(t[x].ls)ans+=query(t[x].ls);
	if(t[x].rs)ans+=query(t[x].rs);
	return ans;
}
signed main()
{
	int n,m;
	read(n),read(m);
	for(int i=1;i<=n;i++)
	{
		read(ori[i].d[0]),read(ori[i].d[1]),read(ori[i].val);
	}
	int root=build(1,n,0);
	for(int i=1;i<=m;i++)
	{
		read(a),read(b),read(c);
		cout<<query(root)<<endl;
	}
	return 0;
}

插入重构

插入

上面只是简简单单的静态的建树，如果我要插入点，你该怎么办？

首先，由于k-D Tree具有二叉搜索树的形态，插入的时候只需要和 当前节点的对应维度坐标 作比较即可，如果小于等于当前节点的第 \(d\) 维，则走向左子树，否则走向右子树。

维度的切换和交替建树一样，\(1\) 到 \(K\) 轮流来即可。

例如，我要将 \((5,0)\) 插入这棵树中。

从 \((2,3)\) 开始，比较第 \(1\) 维，\(5\gt 2\)，走向右子树。

到达 \((4,1)\)，比较第 \(2\) 维，\(0\lt 1\)，走向左子树。

到达 \((3,1)\)，比较第 \(1\) 维，\(5\gt 3\)，走向右子树。

这样一来，插入操作就成功了，吗？

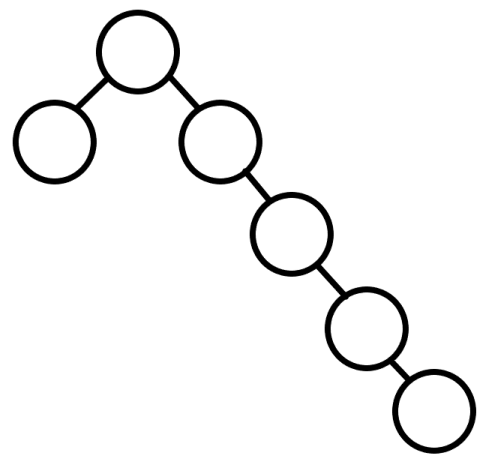
如果我疯狂插入几次极端的点，k-D Tree就有可能变成这样，层数就不再是 \(\log n\) 了，这时候该怎么办呢？重构！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void insert(int &p,node temp,int k)//k为比较维度
{
	if(!p)//k-D Tree中没这个点，直接插入
	{
		p=newnode();//给个新的编号
		t[p]=temp;
		t[p].rs=0,t[p].ls=0;//这步非常重要，不然左右儿子信息会混乱
		update(p);//上传信息
		return;
	}
	if(temp.d[k]<=t[p].d[k])insert(t[p].ls,temp,k^1);//插进左子树
	else insert(t[p].rs,temp,k^1);//插进右子树
	update(p);//上传信息
	check(p,k);//判断是否失衡
    //注意要先update()再check()
}

怎么判断是否需要重构？类似 替罪羊树（没学过也没关系，我也没学过），我们引入一个 平衡因子 \(\alpha\) ，如果该节点的左子树或者右子树的子树大小超过整颗子树大小的 \(\alpha\) 倍，即 \(sz[p]*\alpha<max(sz[ls],sz[rs])\)，我们就需要进行重构，通常 \(0.6\leq \alpha \leq0.9\)，一般取中间值 \(0.75\)，可以根据喜好自己调。

在 update() 函数中，我们需要额外维护子树的大小。

暴力重构

类似静态建树，我们把失衡的子树拍成一个序列，重新对当前子树建树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
bool cmp(int a,int b)//比较的函数有所改变
{
	return t[a].d[K]<t[b].d[K];
}
void pia(int p)
{
	if(!p)return;
	pia(t[p].ls);
    g[++tot]=p;//把当前节点添到序列中
	pia(t[p].rs);
}
void update(int p)
{
    ...
    t[p].sz=t[ls].sz+t[rs].sz+1;
}
int rebuild(int l,int r,int k)//类似静态建树 ，参数有所改变
{
	if(l>r)return 0;
	int mid=(l+r)>>1;
	K=k;
	nth_element(g+l,g+mid,g+r+1,cmp);//注意这里传的是拍出的序列
	t[g[mid]].ls=rebuild(l,mid-1,k^1);
	t[g[mid]].rs=rebuild(mid+1,r,k^1);
	update(g[mid]);
	return g[mid];
}
void check(int &p,int k)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	if(A*t[p].sz<max(t[ls].sz,t[rs].sz))//A为平衡因子
	{
		tot=0;//清空序列
		pia(p);//把以p为根的子树拍成序列，方便重构
		p=rebuild(1,tot,k);//暴力重构，并更新p点编号
	}
}

再来一道例题！

洛谷 P4148 简单题

给一个 \(N\times N\) 的棋盘，每个格子里有一个整数，初始时都为 \(0\)，现在需要维护两种操作：

1 x y A 将格子 x，y 里的数字加上 \(A\)。

2 x1 y1 x2 y2 输出 \(x1,y1,x2,y2\) 这个矩形内的数字和。

\(N\leq5\times10^5\)

强制在线，内存限制 \(20MB\)

非常酷的题，强制在线卡掉了 CDQ分治，内存限制 \(20MB\) 卡掉了树套树，还是老实用k-D Tree吧！

观察到 \(N\) 非常大，我们不可能把棋盘中每个点加到k-d Tree中。由于初始时每个点的值都是 \(0\)，我们考虑操作 \(1\)，给 \((x,y)\) 上的点加上 \(A\) 可以看作在 \((x,y)\) 插入一个权值为 \(A\) 的点。如果我给同一个位置加两次怎么办呢？我们可以把它看作两个不同的点，因为我们查询的是矩形内的数字和，把同一个位置拆开并不影响答案。

插入操作解决了，现在考虑如何查询。

如果当前节点维护的区域完全被询问的矩形包含，那说明它子树中的所有节点都被包含，直接返回权值和。

如果当前节点维护的区域和询问的矩形完全没有交集，那说明它子树中的所有节点都不在矩形中，直接返回 \(0\)。

如果当前节点维护的点在矩形内，给答案加上这个点的权值。

剩下的就可以直接递归该节点的左右子树，累加答案即可。

1
2
3
4
5
6
7
8
int query(int p)
{
	if((!p)|| t[p].mn[0]>X2 || t[p].mx[0]<X1 || t[p].mn[1]>Y2 || t[p].mx[1]<Y1)return 0;//没交集
	if(t[p].mn[0]>=X1 && t[p].mx[0]<=X2 && t[p].mn[1]>=Y1 && t[p].mx[1]<=Y2)return t[p].sum;//被完全包含
	int ans=0;
	if(t[p].d[0]>=X1 && t[p].d[0]<=X2 && t[p].d[1]>=Y1 && t[p].d[1]<=Y2)ans+=t[p].val;//维护的点在矩形中
	return query(t[p].ls)+query(t[p].rs)+ans;//递归左右子树
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
#include<bits/stdc++.h>
using namespace std;
const int MAX=2e5+5;
int K=0,last_ans=0,N=0,cur=0,tot=0;
int X1,X2,Y1,Y2;
double A=0.75;
int g[MAX];
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
struct node
{
	int d[2];
	int mx[2],mn[2];
	int sum,val,sz;
	int ls,rs;
}t[MAX];
int newnode()
{
	return ++cur;
}
bool cmp(int a,int b)
{
	return t[a].d[K]<t[b].d[K];
}	
void update(int x)
{
	int ls=t[x].ls;
	int rs=t[x].rs;
	t[x].sz=t[ls].sz+t[rs].sz+1;
	for(int i=0;i<=1;i++)
	{
		t[x].mx[i]=t[x].mn[i]=t[x].d[i];
		if(ls)
		{
			t[x].mx[i]=max(t[x].mx[i],t[ls].mx[i]);
			t[x].mn[i]=min(t[x].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[x].mx[i]=max(t[x].mx[i],t[rs].mx[i]);
			t[x].mn[i]=min(t[x].mn[i],t[rs].mn[i]);
		}
	}
	t[x].sum=t[ls].sum+t[rs].sum+t[x].val;
}
void pia(int p)
{
	if(!p)return;
	pia(t[p].ls);
	g[++tot]=p;
	pia(t[p].rs);
}
int rebuild(int l,int r,int k)
{
	if(l>r)return 0;
	int mid=(l+r)>>1;
	K=k;
	nth_element(g+l,g+mid,g+r+1,cmp);
	t[g[mid]].ls=rebuild(l,mid-1,k^1);
	t[g[mid]].rs=rebuild(mid+1,r,k^1);
	update(g[mid]);
	return g[mid];
}
void check(int &p,int k)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	if(A*t[p].sz<max(t[ls].sz,t[rs].sz))
	{
		tot=0;
		pia(p);
		p=rebuild(1,tot,k);
	}
}
void insert(int &p,node temp,int k)
{
	if(!p)
	{
		p=newnode();
		t[p]=temp;
		t[p].rs=0,t[p].ls=0;
		update(p);
		return;
	}
	if(temp.d[k]<=t[p].d[k])insert(t[p].ls,temp,k^1);
	else insert(t[p].rs,temp,k^1);
	update(p);
	check(p,k);
}
int query(int p)
{
	if((!p)|| t[p].mn[0]>X2 || t[p].mx[0]<X1 || t[p].mn[1]>Y2 || t[p].mx[1]<Y1)return 0;
	if(t[p].mn[0]>=X1 && t[p].mx[0]<=X2 && t[p].mn[1]>=Y1 && t[p].mx[1]<=Y2)return t[p].sum;
	int ans=0;
	if(t[p].d[0]>=X1 && t[p].d[0]<=X2 && t[p].d[1]>=Y1 && t[p].d[1]<=Y2)ans+=t[p].val;
	return query(t[p].ls)+query(t[p].rs)+ans;
}
int main()
{
	int n,root=0;
	read(n);
	while(1)
	{
		int opt;
		read(opt);
		if(opt==1)
		{
			node temp;
			read(temp.d[0]);
			read(temp.d[1]);
			read(temp.val);
			temp.d[0]^=last_ans,temp.d[1]^=last_ans,temp.val^=last_ans;
			insert(root,temp,0);
		}
		if(opt==2)
		{
			read(X1),read(Y1),read(X2),read(Y2);
			X1^=last_ans,X2^=last_ans,Y1^=last_ans,Y2^=last_ans;
			if(X1>X2)swap(X1,X2);
			if(Y1>Y2)swap(Y1,Y2);
			last_ans=query(root);
			cout<<last_ans<<endl;
		}
		if(opt==3)break;
	}
	return 0;
}

查询

最经典的一个询问就是最近点查询，例如已经给了你 \(n\) 个二维平面上的点，现在给你一个点 \(Q\)，问你这 \(n\) 个点中距离 \(Q\) 最近的是哪个。

关于这个距离，欧几里得距离 和 曼哈顿距离 的查询方法都是一样的，只是计算上有所不同，具体的可以例题上解释。

我们回归正题，这个最近点该怎么查询呢？很显然，直接遍历 \(n\) 个点是很不现实的，我们考虑如何从k-D Tree上搜到答案。

剪枝

假如我们当前搜到了k-D Tree上的点 \(p\)，先更新一下最短距离 \(ans=min(ans,dis(p,Q))\)。

接下来递归左子树和右子树，为了降低我们的时间复杂度，我们可以剪枝，具体是这样的。

  1. 分别计算出点 \(Q\) 到点 \(p\) 的左子树和右子树所管辖矩形的距离，记为 \(disls\) 和 \(disrs\)。
  2. 比较 \(disls\) 和 \(disrs\)，如果 \(disls\lt disrs\)，则先递归左子树，否则先递归右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void query(int p)
{
	ans=min(ans,dis(p));
	int disls=INF;
	int disrs=INF;
	if(t[p].ls)disls=dismatrix(t[p].ls);//计算查询点到左子树管辖矩形的距离
	if(t[p].rs)disrs=dismatrix(t[p].rs);//计算查询点到右子树管辖矩形的距离
	if(disls<disrs)
	{
		if(disls<ans)query(t[p].ls);//先递归左子树
		if(disrs<ans)query(t[p].rs);
	}
	else
	{
		if(disrs<ans)query(t[p].rs);//先递归右子树
		if(disls<ans)query(t[p].ls);
	}
}

可以发现，如果我们先递归左子树，更新了答案以后，如果右子树管辖矩形到查询点的距离大于已更新的答案，就直接跳过了，这样我们就完美地做到了剪枝。

洛谷 P4169 [Violet] 天使玩偶/SJY摆棋子

在二维平面上，给出 \(n\) 个点 \((x,y)\)，以及 \(m\) 个操作。

1 x y 添加一个点 \((x,y)\)。

2 x y 查询所有点中，距离 \((x,y)\) 最近的一个点。

本题中，距离指曼哈顿距离，即 \(dist(A,B)=|A_x-B_x|+|A_y-B_y|\)

本题有插入操作，不能静态建树，需要考虑插入新点后是否重构。

现在考虑如何查询，其实就是上面那个过程，主要难点在如何求出某个点到矩形的曼哈顿距离。

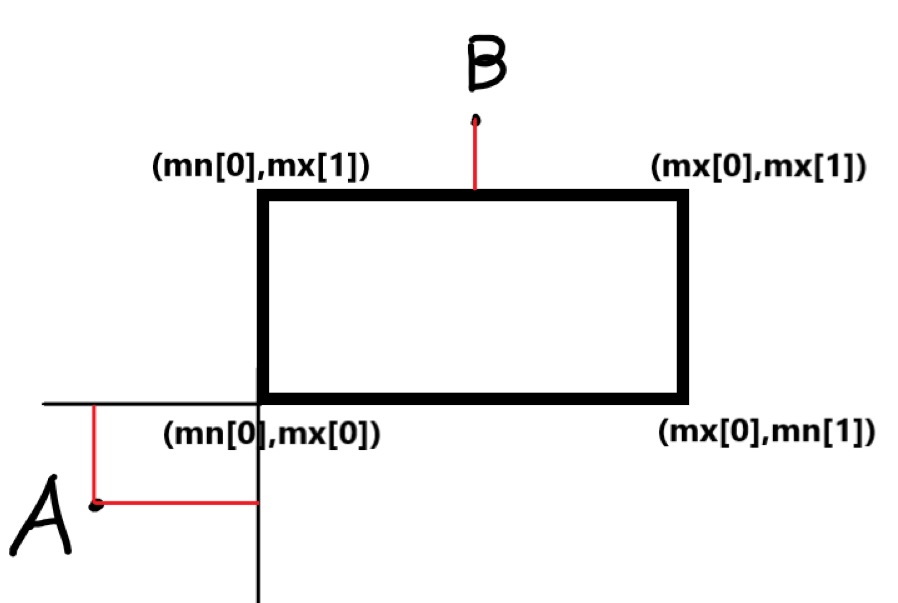
看这张美丽的图，假设 \(A,B\) 是我们给出的查询点，这个矩形是某个子树所管辖的矩形，看图稍微推一下，我们可以这样计算它们的距离：

1
2
3
4
5
6
7
8
int dismatrix(int p)
{
    //(X,Y)为查询点
	int res=0;
	res+=max(0,X-t[p].mx[0])+max(0,t[p].mn[0]-X);
	res+=max(0,Y-t[p].mx[1])+max(0,t[p].mn[1]-Y);
	return res;
}

对于更高维的，我们给出这样一个公式

\(dist(T,P)=\sum_{i=0}^{K-1}max(0,T_i-P_{mx_i})+max(0,P_{mn_i}-T_i)\)

\(T\) 为查询点，\(P\) 为矩形，\(K\)为维度。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e6+5;
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
int K=0,cur=0,cnt=0,X,Y,ans;
double A=0.75;
struct node
{
	int d[2];
	int mn[2],mx[2];
	int sz,ls,rs;
}t[MAX];
int g[MAX];
bool cmp(int a,int b)
{
	return t[a].d[K]<t[b].d[K];
}
void update(int p)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	for(int i=0;i<=1;i++)
	{
		t[p].mx[i]=t[p].mn[i]=t[p].d[i];
		if(ls)
		{
			t[p].mx[i]=max(t[p].mx[i],t[ls].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[p].mx[i]=max(t[p].mx[i],t[rs].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[rs].mn[i]);
		}
	}
	t[p].sz=t[ls].sz+t[rs].sz+1;
}
void pia(int p)
{
	if(!p)return;
	pia(t[p].ls);
	g[++cnt]=p;
	pia(t[p].rs);
}
int rebuild(int l,int r,int k)
{
	if(l>r)return 0;
	K=k;
	int mid=(l+r)>>1;
	nth_element(g+l,g+mid,g+r+1,cmp);
	t[g[mid]].ls=rebuild(l,mid-1,k^1);
	t[g[mid]].rs=rebuild(mid+1,r,k^1);
	update(g[mid]);
	return g[mid];
}
void check(int &p,int k)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	if(t[p].sz*A<max(t[ls].sz,t[rs].sz))
	{
		cnt=0;
		pia(p);
		p=rebuild(1,cnt,k);
	}
}
void insert(int &p,node temp,int k)
{
	if(!p)
	{
		p=++cur;
		t[p]=temp;
		t[p].ls=t[p].rs=0;
		update(p);
		return;
	}
	if(temp.d[k]<=t[p].d[k])insert(t[p].ls,temp,k^1);
	else insert(t[p].rs,temp,k^1);
	update(p);
	check(p,k);
}
int dismatrix(int p)
{
	int res=0;
	res+=max(0,X-t[p].mx[0])+max(0,t[p].mn[0]-X);
	res+=max(0,Y-t[p].mx[1])+max(0,t[p].mn[1]-Y);
	return res;
}
int dis(int p)
{
	return abs(t[p].d[0]-X)+abs(t[p].d[1]-Y);
}
void query(int p)
{
	ans=min(ans,dis(p));
	int disls=1e9;
	int disrs=1e9;
	if(t[p].ls)disls=dismatrix(t[p].ls);
	if(t[p].rs)disrs=dismatrix(t[p].rs);
	if(disls<disrs)
	{
		if(disls<ans)query(t[p].ls);
		if(disrs<ans)query(t[p].rs);
	}
	else
	{
		if(disrs<ans)query(t[p].rs);
		if(disls<ans)query(t[p].ls);
	}
}
int main()
{
	//freopen("tmp.in","r",stdin);
	//freopen("tmp.out","w",stdout);
	int n,m,root=0;
	read(n),read(m);
	int opt;
	for(int i=1;i<=n;i++)
	{
		node temp;
		read(temp.d[0]),read(temp.d[1]);
		insert(root,temp,0);
	}
	for(int i=1;i<=m;i++)
	{
		read(opt);
		if(opt==1)
		{
			node temp;
			read(temp.d[0]),read(temp.d[1]);
			insert(root,temp,0);
		}
		if(opt==2)
		{
			read(X),read(Y);
			ans=1e9;
			query(root);
			printf("%d\n",ans);
		}
	}
	return 0;
}

K-D Tree进阶

了解了k-D Tree的基本用法，接下来看 \(3\) 个例题，来提升一下对k-D Tree的理解，同时学习一下其它的高级查询。

最小最大距离最小距离差

洛谷 P2479 [SDOI2010] 捉迷藏

二维平面上，给出 \(n\) 个点 \((x,y)\) ，请找出一个点，使得该点到其它点的最大距离和该点到其它点的最小距离之差最小，输出编号。

本题中，距离指曼哈顿距离，即 \(dist(A,B)=|A_x-B_x|+|A_y-B_y|\)

由于没有插入操作，静态建树即可。

假设我们现在只查询最小距离，直接枚举 \(n\) 个点，依次查询最小距离即可，注意要给枚举的这个点打个标记，在查询过程中不要查询这个点。

最大距离其实也很容易解决，和查询最小距离反着来即可，注意这时查询点到矩形的距离要取更远的那一个，否则会漏掉答案。

非常好，那就简单了，我们直接枚举 \(n\) 个点，查询出到每个点的最大距离和最小距离，直接更新答案，即 \(ans=min(ans,maxdis-mindis)\)。

代码实现起来比较麻烦，细节较多。

放一下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAX=1e5+5;
const int INF=1e18;
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
int K=0,maxdis,mindis,X,Y;
int ABS(int x)
{
	return (x<0?(-x):x);
}
struct node
{
	int d[2],mx[2],mn[2];
	int ls,rs;
	bool del=0;
}t[MAX],ori[MAX];
bool cmp(node a,node b)
{
	return a.d[K]<b.d[K];
}
void update(int p)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	for(int i=0;i<=1;i++)
	{
		t[p].mx[i]=t[p].mn[i]=t[p].d[i];
		if(ls)
		{
			t[p].mx[i]=max(t[p].mx[i],t[ls].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[p].mx[i]=max(t[p].mx[i],t[rs].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[rs].mn[i]);
		}
	}
}
int build(int l,int r,int k)
{
	if(l>r)return 0;
	K=k;
	int mid=(l+r)>>1;
	nth_element(ori+l,ori+mid,ori+r+1,cmp);
	t[mid]=ori[mid];
	t[mid].ls=build(l,mid-1,k^1);
	t[mid].rs=build(mid+1,r,k^1);
	update(mid);
	return mid;
}
int dis(int p)
{
	return ABS(t[p].d[0]-X)+ABS(t[p].d[1]-Y);
}
int dismatrixmin(int p)
{
	int res=0;
	res+=max((long long)0,X-t[p].mx[0])+max((long long)0,t[p].mn[0]-X);
	res+=max((long long)0,Y-t[p].mx[1])+max((long long)0,t[p].mn[1]-Y);
	return res;
}
int dismatrixmax(int p)
{
	int res=0;
	res+=max((long long)0,t[p].mx[0]-X)+max((long long)0,X-t[p].mn[0]);
	res+=max((long long)0,t[p].mx[1]-Y)+max((long long)0,Y-t[p].mn[1]);
	return res;
}
void querymin(int p)
{
	if(!t[p].del)mindis=min(mindis,dis(p));
	int dl=INF,dr=INF;
	if(t[p].ls)dl=dismatrixmin(t[p].ls);
	if(t[p].rs)dr=dismatrixmin(t[p].rs);
	if(dl<dr)
	{
		if(dl<mindis)querymin(t[p].ls);
		if(dr<mindis)querymin(t[p].rs);
	}
	else
	{
		if(dr<mindis)querymin(t[p].rs);
		if(dl<mindis)querymin(t[p].ls);
	}
}
void querymax(int p)
{
	if(!t[p].del)maxdis=max(maxdis,dis(p));
	int dl=-INF,dr=-INF;
	if(t[p].ls)dl=dismatrixmax(t[p].ls);
	if(t[p].rs)dr=dismatrixmax(t[p].rs);
	if(dl>dr)
	{
		if(dl>maxdis)querymax(t[p].ls);
		if(dr>maxdis)querymax(t[p].rs);
	}
	else
	{
		if(dr>maxdis)querymax(t[p].rs);
		if(dl>maxdis)querymax(t[p].ls);
	}
}
signed main()
{
	int n,root=0,ans=INF;
	read(n);
	for(int i=1;i<=n;i++)read(ori[i].d[0]),read(ori[i].d[1]);
	root=build(1,n,0);
	for(int i=1;i<=n;i++)
	{
		t[i].del=1;
		X=t[i].d[0],Y=t[i].d[1];
		maxdis=-INF,mindis=INF;
		querymin(root),querymax(root);
		/*cout<<t[i].mn[0]<<" "<<t[i].mn[1]<<" "<<t[i].mx[0]<<" "<<t[i].mx[1]<<endl;
		cout<<"ls"<<t[i].ls<<endl;
		cout<<"rs"<<t[i].rs<<endl;*/
		ans=min(ans,maxdis-mindis);
		t[i].del=0;
	}
	cout<<ans<<endl;
	return 0;
}

\(k\) 远距离查询

洛谷 P2093 [国家集训队] JZPFAR

二维平面上有 \(n\) 个点 \((x,y)\)，现有 \(m\) 次询问，每次询问给出一个点 \((px,py)\) 以及 \(k\)，查询这 \(n\) 个点中到点 \((px,py)\) 的距离第 \(k\) 大的点的编号。如果有多个点到 \((px,py)\) 的距离相同，那么认定编号较小的点距离较大。

本题中，距离指欧几里得距离，即 \(dist(A,B)=\sqrt {(A_x-B_x)^2+(A_y-B_y)^2}\)

是个麻烦题。首先，为了方便，我们在计算距离时可以不用开方，不影响答案。

由于没有插入操作，静态建树即可。

查询最大距离就不用说了，之前提过了，现在考虑怎么统计第 \(k\) 远。

我们可以开一个 小根堆，先插入 \(k\) 个极小值，然后从根节点开始查询，如果 \((px,py)\) 到当前节点的距离大于堆顶存的距离，或者 \((px,py)\) 到当前节点的距离等于堆顶存的距离，但是该点编号小于堆顶存的编号，我们就弹出堆顶，把现在这个点到 \((px,py)\) 的距离和这个点的编号丢进去。查询结束后，堆顶存的编号就是答案。

具体过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct ans
{
	int dis,id;
};
bool operator <(ans a,ans b)
{
	if(a.dis==b.dis)return a.id<b.id;
	return a.dis>b.dis;
}
priority_queue<ans>q;
void query(int p)
{
	if(!p)return;
	int dis=getdis(t[p].d[0],t[p].d[1],X,Y);//获取当前点到查询点的距离
	if(dis>q.top().dis || (dis==q.top().dis && t[p].id<q.top().id))//距离更远
	{
		q.pop();
		q.push({dis,t[p].id});//把更远的丢进堆
	}
    //剪枝优化
	int dl=-INF,dr=-INF;
	if(t[p].ls)dl=dismatrix(t[p].ls);
	if(t[p].rs)dr=dismatrix(t[p].rs);
	if(dl>dr)
	{
		if(dl>=q.top().dis)query(t[p].ls);
		if(dr>=q.top().dis)query(t[p].rs);
	}
	else
	{
		if(dr>=q.top().dis)query(t[p].rs);
		if(dl>=q.top().dis)query(t[p].ls);
	}
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAX=1e6+5;
const int INF=1e18;
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
struct node
{
	int d[2],mx[2],mn[2];
	int ls,rs;
	int id;
}t[MAX],ori[MAX];
struct ans
{
	int dis,id;
};
bool operator <(ans a,ans b)
{
	if(a.dis==b.dis)return a.id<b.id;
	return a.dis>b.dis;
}
priority_queue<ans>q;
int K=0,X,Y;
bool cmp(node a,node b)
{
	return a.d[K]<b.d[K];
}
void update(int p)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	for(int i=0;i<=1;i++)
	{
		t[p].mx[i]=t[p].mn[i]=t[p].d[i];
		if(ls)
		{
			t[p].mx[i]=max(t[p].mx[i],t[ls].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[p].mx[i]=max(t[p].mx[i],t[rs].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[rs].mn[i]);
		}
	}
}
int build(int l,int r,int k)
{
	if(l>r)return 0;
	K=k;
	int mid=(l+r)>>1;
	nth_element(ori+l,ori+mid,ori+r+1,cmp);
	t[mid]=ori[mid];
	t[mid].ls=build(l,mid-1,k^1);
	t[mid].rs=build(mid+1,r,k^1);
	update(mid);
	return mid;
}
int getdis(int x1,int y1,int x2,int y2)
{
	int k1=(x1-x2)*(x1-x2);
	int k2=(y1-y2)*(y1-y2);
	return k1+k2;
}
int dismatrix(int p)
{
	int dis=-INF;
	dis=max(dis,getdis(t[p].mn[0],t[p].mn[1],X,Y));
	dis=max(dis,getdis(t[p].mx[0],t[p].mn[1],X,Y));
	dis=max(dis,getdis(t[p].mx[0],t[p].mx[1],X,Y));
	dis=max(dis,getdis(t[p].mn[0],t[p].mx[1],X,Y));
	return dis;
}
void query(int p)
{
	if(!p)return;
	int dis=getdis(t[p].d[0],t[p].d[1],X,Y);
	if(dis>q.top().dis || (dis==q.top().dis && t[p].id<q.top().id))
	{
		q.pop();
		q.push({dis,t[p].id});
	}
	int dl=-INF,dr=-INF;
	if(t[p].ls)dl=dismatrix(t[p].ls);
	if(t[p].rs)dr=dismatrix(t[p].rs);
	if(dl>dr)
	{
		if(dl>=q.top().dis)query(t[p].ls);
		if(dr>=q.top().dis)query(t[p].rs);
	}
	else
	{
		if(dr>=q.top().dis)query(t[p].rs);
		if(dl>=q.top().dis)query(t[p].ls);
	}
}
signed main()
{
	int n,m,k;
	read(n);
	for(int i=1;i<=n;i++){read(ori[i].d[0]),read(ori[i].d[1]);ori[i].id=i;}
	int root=build(1,n,0);
	read(m);
	for(int i=1;i<=m;i++)
	{
		read(X),read(Y),read(k);
		while(!q.empty())q.pop();
		for(int i=1;i<=k;i++)q.push({-INF,INF});
		query(root);
		cout<<q.top().id<<endl;
	}
	return 0;
}

圆的相交问题

洛谷 P4631 [APIO2018] 选圆圈

在二维平面上，有 \(n\) 个圆，记为 \(c_1,c_2,...,c_n\)。执行以下操作：

  1. 找到这些圆中半径最大的。如果有多个半径最大的圆，选择编号最小的。记为 \(c_i\)。
  2. 删除 \(c_i\) 及与其有交集的所有圆。两个圆有交集当且仅当平面上存在一个点，这个点同时在这两个圆的圆周上或圆内。
  3. 重复上面两个步骤直到所有的圆都被删除。

当 \(c_i\) 被删除时，若循环中第 \(1\) 步选择的圆是 \(c_j\)，我们说 \(c_i\)被 \(c_j\) 删除。对于每个圆，求出它是被哪一个圆删除的。

样例：

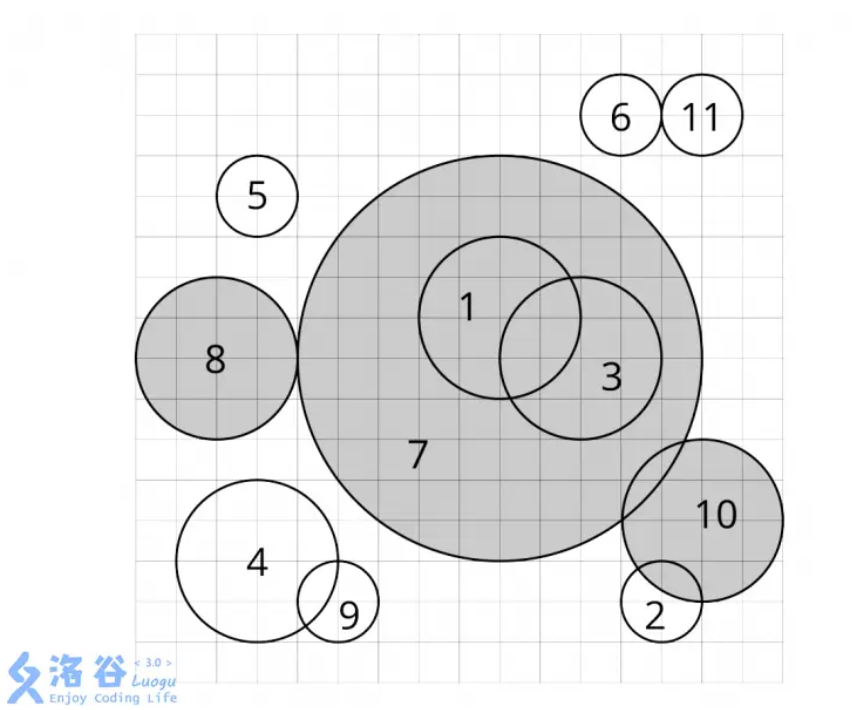
1
2
3
4
5
6
7
8
9
10
11
12
11
9 9 2
13 2 1
11 8 2
3 3 2
3 12 1
12 14 1
9 8 5
2 8 2
5 2 1
14 4 2
14 14 1
1
7 2 7 4 5 6 7 7 4 7 6

样例解释：

有圆，不太好处理，看起来无从下手？

我们不妨把每个圆看成矩形（即边长为 \(2r\) 的正方形），那么很容易得出，如果两个矩形没有交集，那么这两个矩形代表的圆一定没有交集。

那么怎么储存每个圆的信息呢？还是k-D Tree，这时我们每个节点维护的信息比较多。

1
2
3
4
5
6
7
8
9
10
11
struct circle
{
	int d[2];//圆的坐标
	int r,id;//半径和编号
}c[MAX];
struct node
{
	circle dat;//该点代表的圆
	int mx[2],mn[2];//近似矩形
	int ls,rs;//左右儿子
}t[MAX];

矩形很好维护，只是四个顶点的坐标和之前有所不同，用圆的半径和坐标计算即可。

由于没有插入操作，静态建树即可。

接下来是比较关键的内容，如何查询哪些圆与当前圆相交。

首先是判断圆与圆是否有交集，比较好推，也是一个比较常见的结论。

对于两个圆 \(A,B\)，它们圆心的距离为 \(dist(A,B)=\sqrt {(A_x-B_x)^2+(A_y-B_y)^2}\)，如果它们的半径和大于等于圆心之间的距离，说明它们相交或者相切，即有交集。为了防止出现精度问题，我们可以在式子两边平方一下，得到判定式：

\((A_x-B_x)^2+(A_y-B_y)^2\leq (A_r+B_r)^2\)

假设我们当前查询到了k-D Tree上的点 \(p\)，如果 \(p\) 管辖的矩形和查询圆的近似矩形没有交集，说明 \(p\) 子树内的所有圆一定和查询圆没有交集，直接返回。否则就看 \(p\) 维护的圆和查询圆是否有交集，同时 \(p\) 点维护的圆没有被删除，那就统计答案，并递归左右子树继续统计答案。

至于怎么判断两个矩形是否相交，条件较多，我们不妨判断两个矩形是否不相交：

  • 如果矩形 \(A\) 最右端小于矩形 \(B\) 最左端，则两个矩形不相交。
  • 如果矩形 \(A\) 最左端大于矩形 \(B\) 最右端，则两个矩形不相交。
  • 如果矩形 \(A\) 最上端小于矩形 \(B\) 最下端，则两个矩形不相交。
  • 如果矩形 \(A\) 最下端大于矩形 \(B\) 最上端，则两个矩形不相交。

完整代码 （不要复制哦）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include<bits/stdc++.h>
using namespace std;
#define int long long
template<typename T>
void read(T &x)
{
	x=0;
	int f=1;
	char ch=getchar();
	while(!isdigit(ch))
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch))
	{
		x=x*10+(ch^48);
		ch=getchar();
	}
	x*=f;
}
const int MAX=1e6+5;
struct circle
{
	int d[2];
	int r,id;
}c[MAX];
struct node
{
	circle dat;
	int mx[2],mn[2];
	int ls,rs;
}t[MAX];
int K=0;
int ans[MAX];
bool cmp(circle a,circle b)
{
	return a.d[K]<b.d[K];
}
bool recmp(circle a,circle b)
{
	if(a.r==b.r)return a.id<b.id;
	return a.r>b.r;
}
void update(int p)
{
	int ls=t[p].ls;
	int rs=t[p].rs;
	for(int i=0;i<=1;i++)
	{
		t[p].mn[i]=t[p].dat.d[i]-t[p].dat.r;
		t[p].mx[i]=t[p].dat.d[i]+t[p].dat.r;
		if(ls)
		{
			t[p].mx[i]=max(t[p].mx[i],t[ls].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[ls].mn[i]);
		}
		if(rs)
		{
			t[p].mx[i]=max(t[p].mx[i],t[rs].mx[i]);
			t[p].mn[i]=min(t[p].mn[i],t[rs].mn[i]);
		}
	}
}
int build(int l,int r,int k)
{
	if(l>r)return 0;
	K=k;
	int mid=(l+r)>>1;
	nth_element(c+l,c+mid,c+r+1,cmp);
	t[mid].dat=c[mid];
	t[mid].ls=build(l,mid-1,k^1);
	t[mid].rs=build(mid+1,r,k^1);
	update(mid);
	return mid;
}
bool intersect(circle a,circle b)
{
	int x=a.d[0];
	int y=a.d[1];
	int r=a.r;
	int sec1=(x-b.d[0])*(x-b.d[0]);
	int sec2=(y-b.d[1])*(y-b.d[1]);
	int sec3=(r+b.r)*(r+b.r);
	if(sec1+sec2<=sec3)return 1;
	return 0;
}
bool dismeet(int p,circle temp)
{
	int L=temp.d[0]-temp.r;
	int R=temp.d[0]+temp.r;
	int U=temp.d[1]+temp.r;
	int D=temp.d[1]-temp.r;
	if(R<t[p].mn[0])return 1;
	if(U<t[p].mn[1])return 1;
	if(L>t[p].mx[0])return 1;
	if(D>t[p].mx[1])return 1;
	return 0;
}
void query(int p,circle temp)
{
	if(dismeet(p,temp))return;
	if(intersect(t[p].dat,temp) && !ans[t[p].dat.id])ans[t[p].dat.id]=temp.id;
	int ls=t[p].ls;
	int rs=t[p].rs;
	if(ls)query(ls,temp);
	if(rs)query(rs,temp);
}
signed main()
{
	int n;
	read(n);
	for(int i=1;i<=n;i++)
	{
		read(c[i].d[0]),read(c[i].d[1]),read(c[i].r);
		c[i].id=i;
	}
	int root=build(1,n,0);
	sort(c+1,c+n+1,recmp);
	for(int i=1;i<=n;i++)if(!ans[c[i].id])query(root,c[i]);
	for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
	return 0;
}

总结

如果读者想牢记这个算法，请最好按照我的写法来，记忆起来非常方便，并且思路比较清晰。感谢观看。